End-to-end FE based homogenization of woven composites
Background and Motivation
The large amount of woven designs is still found where tailor made, high-end solutions are needed and a costly solution is acceptable. The applications cover the Aerospace, Automotive (racing), Marine, wind technology and sport equipment markets. The overall objective is to use light-weight materials with the best stiffness and strength properties possible.
Woven composites are typically draped onto more or less complex surfaces to produce structural parts. The draping process can have significant impact on local warp and weft angles which leads to a local variation of effective material properties. Understanding the connection between the warp / weft microstructure, the resulting material properties and finally their influence on the part performance is crucial knowledge in the design process of woven composite structure.
A key challenge in the predictions of the woven behavior is the modeling of the mechanical behavior of a single ply. This paper presents our end-to-end FE based homogenization and Digimat mean-field homogenization for woven, braided and 2.5D woven. Comparison is made with experimental results for three different descriptions of woven.
FE based homogenization of woven
End-to-end solution
A complete end-to-end solution has been implemented in Digimat®. It allows performing all the different steps needed to obtain a complete FE analysis, starting from the material data available in the datasheet of the considered woven fabric. Those steps are:
- Mean-field homogenization of the yarns
- Generation of a geometry of a unit cell
- Generation of a RVE
- Voxelisation
- FE model definition and application of periodic boundary conditions
- Solving the FE analysis
- Post-processing the outputs of the FE analysis.
Generation of the geometry of woven, braided and 2.5D woven
Based on the description of the woven (weave pattern, yarn cross section dimension, yarn density in the woven), a geometrical model of each yarn is built [1]. Those geometries are then assembled to create a unit cell (Figure 1). This unit cell is in turn adjusted in order to create a parallelipipedic RVE out of it. This RVE will then be meshed and used for the FE analysis.
Voxelisation
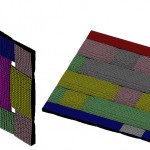
The geometry is discretized with a regular pattern of 8-node brick finite elements. This pattern is known as a voxel mesh (volume and pixel). Each element is assigned to the material of the phase where its center is located: either in the matrix material or in the homogenized yarn material. In the latter case, the local orientation is mapped from the geometry to the yarn element. Such a voxel mesh is illustrated on Figure 3, where the matrix elements are hidden.
In a voxel mesh, the boundary between the matrix element set and the yarn element set is a patch of rectangular facets that are parallel to one of the RVE faces. It may then be regarded as a less accurate approximation to the RVE inner surfaces than the one that would be obtained with a usual tetrahedral mesh generator with nodes exactly on the surfaces. Still, this approach is more robust than that alternative which leads to badly-shaped tetrahedral elements in areas between yarns or close to yarn crossings.
Moreover, the resulting finite element stiffness matrix has a smaller bandwidth and a better conditioning number than with a conventional mesh generator. The linear systems to be solved are well suited to iterative solvers, which we found to be particularly computationally efficient in this work. Consequently, models with small element edges, which represent the geometry sufficiently well, may be solved in a moderate CPU time.
Mean-field homogenization of woven
Mean-Field Homogenization Theory
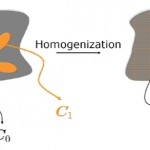
Composites are by definition a combination of two or more constituents to obtain an improved material in comparison to the base constituents. As composite properties depend on the material microstructure including fiber amount and orientation, they are adequately modeled from micromechanics. In particular, mean-field homogenization combines the properties of the underlying constituents of a multi-phase material so that the original heterogeneous material is represented by an equivalent homogeneous one. Implemented in the Digimat software [2], this technology has proven effective for a broad range of materials.
Application to woven
Woven composites rely on a two-step homogenization scheme. The first step consists in the homogenization of the local behavior of the yarn. The latter is modeled as a UD composite. The second step consists in the homogenization of the ply. The latter is described as a matrix reinforced by a large number of inclusions. The orientation, volume fraction and aspect ratio of these inclusions (Figure 5) are computed from the geometry and orientation of the yarn cross sections [1]. Therefore, the set of inclusions takes the yarn waviness into account. A current assumption of our model is that inclusions are represented by a spheroid instead of using an ellipsoid.
Validation of both homogenization procedures
The FE and mean-field homogenizations of woven have been validated on three different types of woven: a balanced plain weave, an unbalanced plain weave and a 5HS satin. For each simulation 3D periodic boundary conditions and the Marc iterative solver are used.
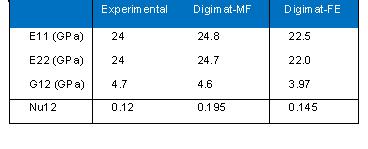
The balanced plain weave glass/epoxy material data come from Lomov [3]. Our predictions with FE homogenization and voxel mesh and with mean field homogenization are compared to experimental data and the FE predictions with conformal mesh obtained by Lomov (Table 1). The yarn width-to-height ratio is equal to 17. The mesh consists of 50*50*20 voxels (Figure 6).

Table 1: Elastic constants of a balanced plain weave glass/epoxy material: experimental measurements and predictions.
Predictions obtained with our two methods of homogenization are close to the experimental measurements and to the predictions of Lomov. The larger discrepancy is observed on the shear modulus predicted by mean-field homogenization. Four simulations have been required to compute these properties. They took altogether a total computation time of 88secs.
The unbalanced plain weave glass/PPS material data come from Angioni [4]. The mesh consists also of 50*50*20 voxels. The ratio between the warp and the weft width is 0.91. The yarn width-to-height ratio is equal to 19. Our predictions with FE homogenization and voxel mesh and with mean field homogenization are compared to experimental data (Table 2).
Table 2: Elastic constants of a unbalanced plain weave glass/PPS material: experimental measurements and predictions.
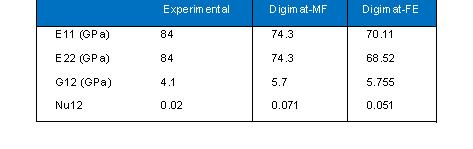
The balanced 5HS T-300 carbon/PPS material data come from Angioni [4]. The mesh consists in 100*100*20 voxels (Figure 6). The yarn width-to-height ratio is equal to 20. Our predictions with FE homogenization and voxel mesh and with mean field homogenization are compared to experimental data (Table 3).
Table 3: Elastic constants of a balanced 5HS T-300 carbon/PPS material: experimental measurements and predictions.
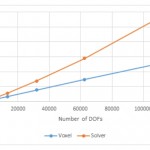
The balanced plain weave model has been used to perform a study over the computation time for the voxelisation and the iterative solver over increasing number of degree of freedom (Figure 7). Both evolve quasi linearly. Less than hundred seconds are needed to obtain results from an input file when hundred thousands of degrees of freedom are involved in the computation.
Conclusions
Digimat® proposes an end-to end FE based homogenization of woven, braided and 2.5D woven composites. A single tool allows generating the geometry, the mesh, run the computation and post-processes the results from material data available in datasheets. The full determination of the elastic constants of a woven material can be obtained in less than 200secs when approximately hundred thousands of degrees of freedom are involved. The voxel mesh allows obtaining meshes for large width-to-height ratio of yarn cross-sections. The same material description can also be used in mean-field homogenization analysis. Predictions of elastic properties of both homogenization methods have been successfully validated against experimental measurements.
Maxime A. Melchior, Marc Duflot, Jean-Sébastien Gerard, Laurent Adam, Roger Assaker – e-Xstream engineering, an MSC Software Company