
Claudio Cappabianca – AIPnD
Davide Baratto, Alberto Anzani – Gilardoni
L’impiego dei materiali compositi nei settori aeronautico e aerospaziale ha avuto un incremento esponenziale dai primi anni ’60 a oggi, grazie alla disponibilità di una vasta varietà dei compositi. L’impiego di questi nuovi materiali ha imposto nel contempo un adeguamento nei controlli non distruttivi sia in fase di costruzione-assemblaggio che nella fase di esercizio. La tomografia, attualmente, è l’unico metodo in grado di fornire informazioni relative alla difettologia, vedi difetti di dislocazione, strutturali, e su aspetti dimensionali anche di elementi complessi. Verranno illustrate alcune applicazioni della tomografia ad alta risoluzione e tomografia 3D su componenti per utilizzi aeronautico e aerospaziale.
La Tomografia (CT)
Il metodo tomografico utilizza sorgenti microfuoco, minifuoco, o convenzionali a raggi X a seconda delle esigenze di risoluzione spaziale e assorbimento dell’oggetto in ispezione. La CT è in grado di ricostruire immagini in 3D per verificare disposizione delle fibre, eventuali difetti interni e/o esterni, misure lineari.
Principi della tomografia
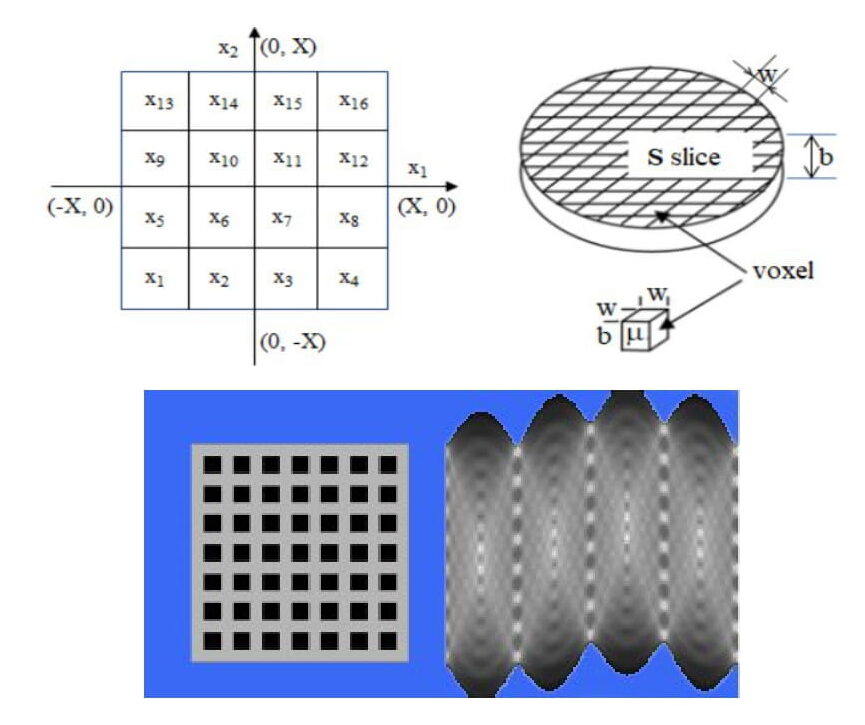
In tutti i tipi di tomografia è sempre identificabile un asse, detto asse tomografico. Alla direzione dell’asse tomografico corrisponde l’asse di rotazione di eventuali parti mobili del tomografo o, nei casi in cui nulla ruota, l’asse di simmetria del sistema, come, ad esempio, l’asse di simmetria degli anelli di rivelatori nella PET. Il volume da ricostruire viene usualmente sezionato in fette, slices, le quali sono perpendicolari all’asse tomografico, slices trasversali (fig.1).
Esse hanno una altezza b, detto spessore della slice. Ogni fetta è suddivisa mediante una griglia cartesiana 2D in pixel quadrati di lato w. Poichè alla slice si associa lo spessore b, i pixel diventano voxel. Un voxel è pertanto un parallelepipedo a sezione quadrata (lato w) nel piano della slice e di altezza b nella direzione dell’asse tomografico. La ricostruzione dei dati tomografici è la determinazione dei valori di densità, ovvero il valore della radiazione in ogni voxel. La risoluzione è funzione della dimensione del voxel.
Risultato finale è la sommatoria di una serie di sezioni non necessariamente contigue di spessore preimpostato: l’insieme delle sezioni ricostruite costituiscono i dati inerenti al volume scansionato ricostruito da un software di rendering tridimensionale. Si possono ottenere immagini relative a qualunque piano spaziale: frontale, sagittale, assiale, o immagini tridimensionali. I processi di ricostruzione per ottenere le immagini dai dati grezzi, rawdata, sono la convoluzione e la retroproiezione, backprojection (trasformata di Radon).
Convoluzione e back projection
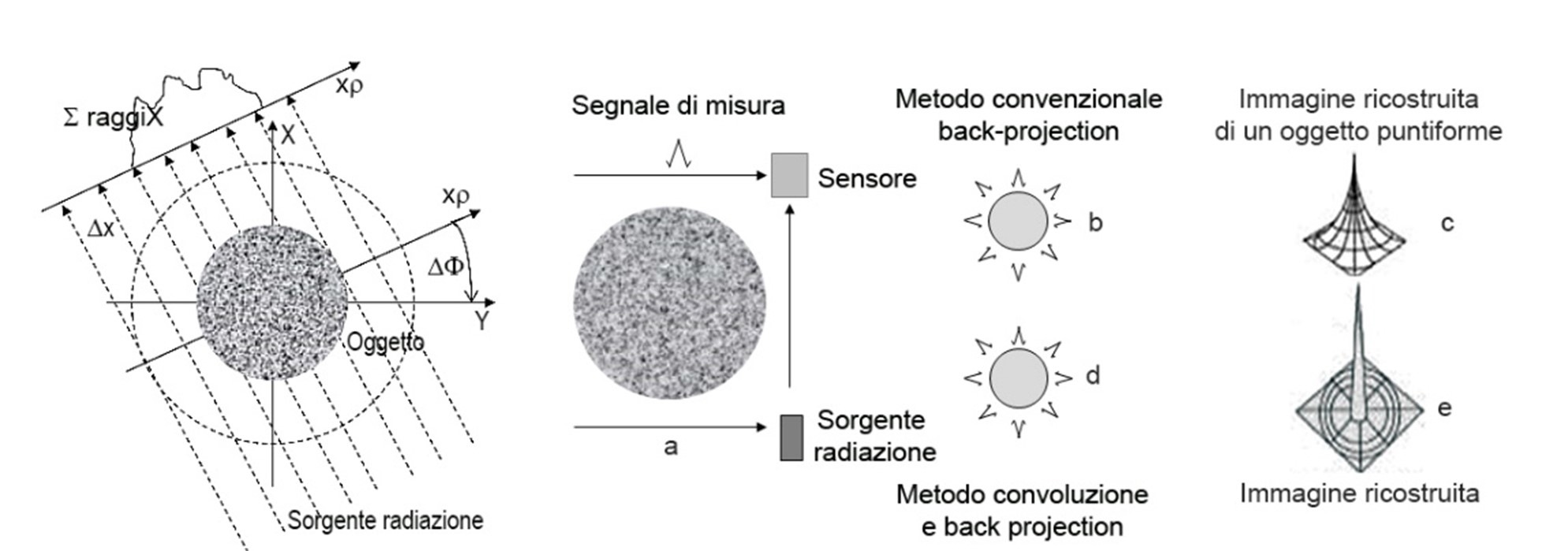
L’attenuazione è il logaritmo naturale del rapporto dell’intensità del fascio incidente del fascio trasmesso, ed è anche indicato come ray-sum. Il processo viene ripetuto N volte ad angoli differenti. L’incremento angolare tra le proiezioni è indicato con Df. L’intervallo angolare totale su cui si ottengono queste proiezioni possono essere limitati a 180°. Un’immagine ricostruita della distribuzione 2D del coefficiente di attenuazione lineare μ(x, y) è ottenuta da queste proiezioni, e in linea di principio è sufficiente notare che il coefficiente di attenuazione lineare è approssimativamente proporzionale alla densità di massa.
Supponiamo di tomografare un oggetto circolare con un inserto centrale a densità differente: la curva di risposta del rivelatore è indicata in a e in b le curve di spostamento in relazione ai vari angoli di ripresa; in c viene mostrata la relativa sommatoria. Come si vede, l’immagine risultante non è puntiforme ma un cono che si allarga. Il metodo ricostruttivo della convoluzione applicata alla backprojection aggiunge un valore negativo che abbatte il valore ottenuto allorchè il fascio di radiazione incontra un oggetto puntiforme o c’è un brusco cambio nel fattore di attenuazione: in e e d il risultato (fig.2).
Matematicamente si passa da un algoritmo del tipo:
∫µ(s) ds = -ln (I/Io)
ad un algoritmo più complesso:
P(q,r) = -ln[I(q,r) ¤ Io]=∫µ(x,y) ds
Dove I rappresenta una singola misura ideale ma indicante anche che il rivelatore è posto rispetto all’oggetto allo stesso angolo q e nella stessa posizione r, Io il livello del segnale non attenuato, m(x,y) è il coefficiente di attenuazione lineare dell’oggetto nelle due dimensioni, ds è la distanza lungo il fascio di radiazione attraversato dall’oggetto all’angolo q e posizione r. I valori di I(q,r) vengono normalizzati all’unità e calcolati in modo tale da ottenere un insieme di linee integrali stimate attraverso l’oggetto P(q,r).
Il processo di convoluzione nel dominio spaziale è equivalente ad una moltiplicazione nel dominio di frequenza.
f (x, y) = g (x, y) X h (x, y)
dove:
- f(x,y) è la sezione ricostruita e filtrata
- g(x,y) è la sezione retroproiettata
- h(x,y) è la funzione filtro.
Sensibilità di contrasto e risoluzione
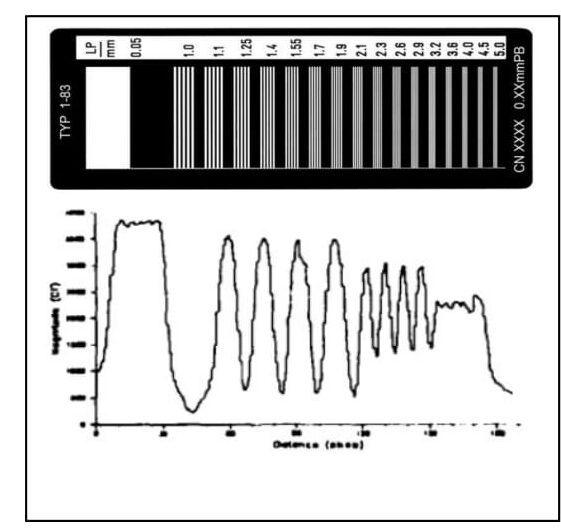
La misura della sensibilità al contrasto si ottiene prendendo una regione nell’immagine ricostruita con campioni di riferimento in Al e calcolando la media e la deviazione standard per tutti i numeri CT nella regione di interesse. Il rapporto tra la media e la deviazione standard viene utilizzato come misura segnale/rumore, indice importante delle prestazioni del sistema (fig.3). Dovendo ispezionare componenti con differenze di assorbimento dei raggi X, vedi il secondo esempio riportato, particolari accorgimenti sono necessari per ottenere una sensibilità di contrasto elevato.
Scansione tomografica su campioni per uso aeronautico
Vengono illustrati due esempi tipici di componenti in composito: due piastre di fibra di carbonio con due difetti introdotti intenzionalmente, e una piastra di alluminio con incollaggio di un substrato di sughero.
Le scansioni sono state eseguite con un tomografo Gilardoni, modello XE-S, dotato di sorgente a raggi-X da 150 kV e macchia focale da 5 µm, detector da 23×23 cm, 12802 pixel, e dimensione del pixel di 179 µm. Con tale apparecchio è possibile ottenere risoluzioni dell’ordine di 10 µm (fig.4).

Esempi di applicazione
Composito con fibre di carbonio.
Dati esposizione
- Energia della radiazione: 100 kV, 68 µA
- Tempo di acquisizione del pannello: 333 ms (3 fps)
- Risoluzione del pannello: 4096 x 4096 px
- Numero di proiezioni: 2500.
La figura 5 mostra una tomografia su una piastra di carbonio da circa 100×150 mm, dove è stato possibile rilevare una cricca negli strati più interni, a 1,2 mm dalla superficie. L’indentazione delle fibre indica che la crepa, lunga circa 60 mm, è stata causata da un urto con un piccolo oggetto ad alta velocità.
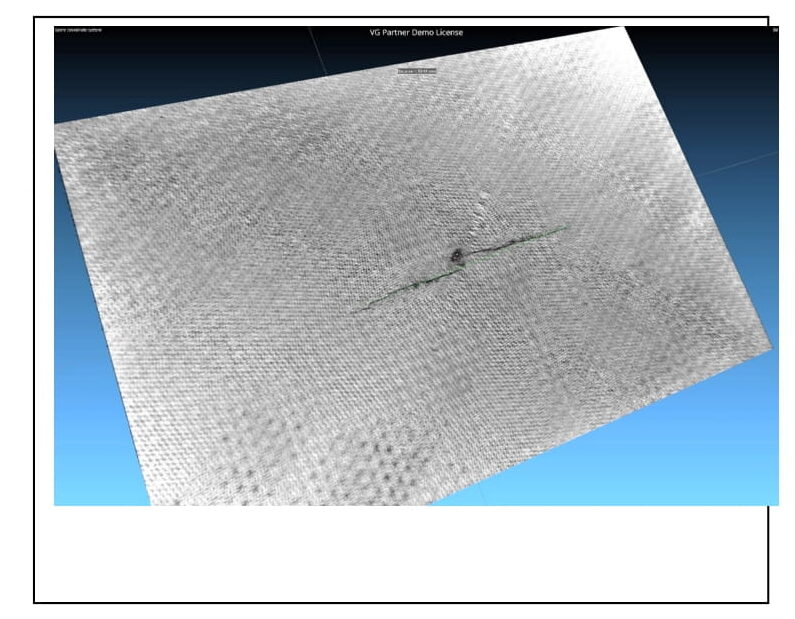
La tomografia di figura 6 su un’altra piastra in carbonio evidenzia invece un difetto nella trama delle fibre, come visibile dalla sezione virtuale effettuata con il software di rendering 3D. Entrambe le tipologie di composito trovano largo uso nei settori aeronautici.
Il campione successivo è invece una piastra di alluminio su cui è incollato una sottile lastra di sughero; il sughero viene utilizzato come barriera termica sulle ogive di razzi.

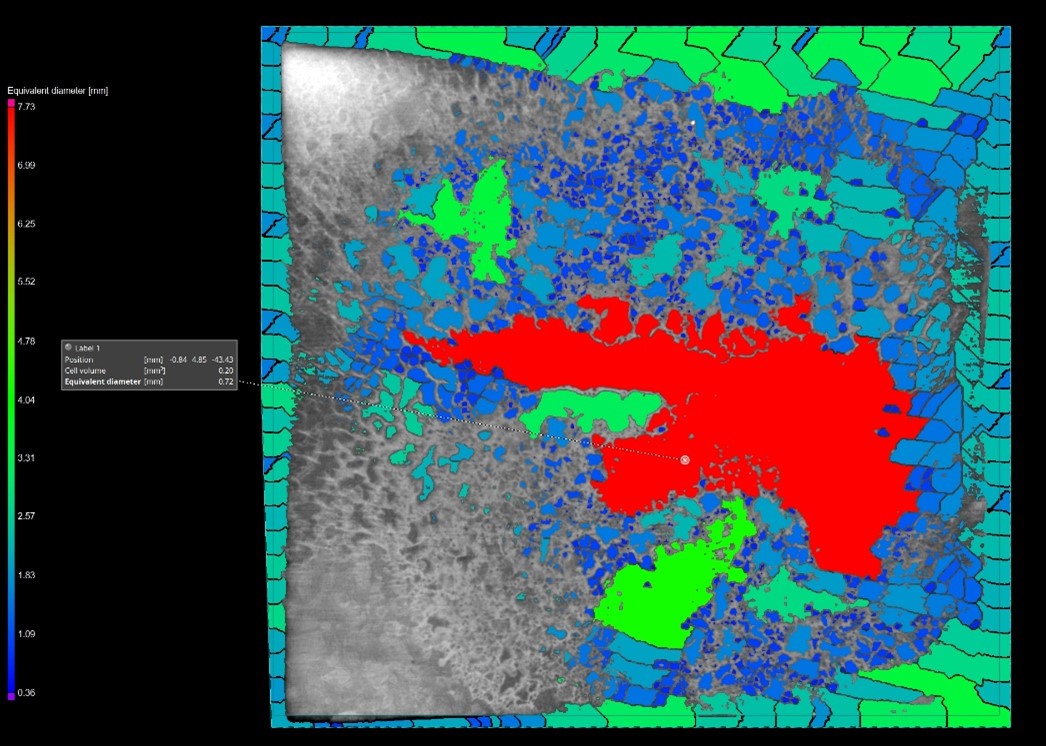
La tomografia, potendo discriminare i due materiali grazie alla loro diversa densità, consente, tra altre cose, di separarli virtualmente; in questo caso, così facendo, è stato possibile osservare lo strato di collante e constatare la presenza di aree in cui questo è assente o insufficiente (fig-6-7-8). Il metodo trova impiego anche nelle giunzioni metallo/ceramica.

Conclusioni
La scansione TC sui pannelli compositi consente l’ispezione di difetti esterni e interni come crepe, protuberanze e disallineamento delle fibre. I pannelli possono essere sezionati virtualmente lungo qualsiasi direzione spaziale e la superficie di sezionamento può essere, oltre a un piano, qualsiasi altra superficie definita dall’utente: ciò significa che, ad esempio, componenti curvi possono essere sezionati utilizzando una superficie curva, consentendo una vista delle strutture interne indipendentemente dalla forma del provino.
Il sistema utilizzato consente di individuare difetti dell’ordine di 30 µm, ma se necessario è possibile utilizzare altre sorgenti con aree focali inferiori per avere risoluzioni fino a pochi micron.
Normative di riferimento
ASTM E1695-20, “Standard Test Method for Measurement of Computed Tomography (CT) System Performance”.
VDI-VDE 2630 part 1.2, 1.3. “Computer tomography in dimensional measurement”
Bibliografia
- The Scientist and Engineer’s Guide to Digital Signal Processing By Steven W. Smith, Ph.D.
- Elements of digital radiography K. Huang Prentice Hall Inc.
- Jackson, L.B., Signal, Systems and Transforms, 1990, p 171. Addison-Wesley, Reading, MA.
- Kak, A.C., and M. Slaney, Principles of Computerized Tomographic Imaging, 1988. IEEE Press, Piscataway, NJ.
- Kittel, C., Introduction to Solid State Physics, 4th ed., 1971, p 66. John Wiley and Sons, New York, NY.
- Rattey, P.A., and A.G. Lindgren, “Sampling the 2-D Radon Transform”, IEEE Transactions on Acoustics, Speech and Signal Processing, Vol. ASSP-29, No. 5, 1981, pp 994-1002.
- Wells, P., J. Davis, and M. Morgan, “Computed Tomography”, Materials Forum, Vol. 18, 1994, pp 111-133.
- Flisch et al. – “Industrial computed tomography in reverse engineering applications”.
- DGZfP-Proceedings BB 67-CD, Paper 8, 1999.
- Obrist et al. – “First article inspection based on industrial X-ray computed tomography”.
- Proceedings of International Conference on material testing and research, 2001, Nuremberg.
- Flisch et al. – “Efficient volume digitizing with adaptive computed tomography”.
- DGZfP-Proceedings BB 84-CD, Paper 17, 2003.
- Sauerwein et al. – “25 years of industrial CT in Europe”, DGZfP-Proceedings BB 84-CD, Paper 10, 2003.
- The Scientist and Engineer’s Guide to Digital Signal Processing By Steven W. Smith, Ph.D.












